Trigonometry is the branch of mathematics
that deals with triangles,
circles,
oscillations
and waves;
it is absolutely crucial to much of geometry
and physics.
You'll often hear it described as if it was all about triangles, but I
think that is missing much of the point. Waves and resonance
are at the root of how matter
works at the mostfundamentallevel;
they are behind how sound
and light
move, and probably also how minds
and beauty
work, on some level; so trigonometry turns out to be fundamental to
pretty much everything. Any time you want to figure out anything to do
with angles,
or turning, or swinging,
there's trigonometry involved.
The first thing to understand with trigonometry is
why the mathematics
of right-angled triangles should also be the mathematics of circles.
Picture a line which can turn around one of its ends, like the hand of
a clock.
Obviously, the moving end of the line traces out a circle - it's like
drawing with a compass.
Now, consider how far this point is to the right or left of the centre
point (we call this distance x), and how far above
or below (which we'll call y). By attaching
horizontal and vertical lines of lengths x and y
to the ends of the first line we get a right-angled triangle, like this:
There
is an applet illustrating this even more clearly here
(part of 'Dave's Short Trig Course').
So the mathematical relationship between circles and
the set of right-angled triangles should be clear: The position (x,
y) of a point at an angle of θ
around a circle of radius r is related to θ
and r in exactly the same way that the lengths of
the adjacent
(x) and opposite
(y) sides of a right-angled triangle are related to
the length of the hypotenuser and the angle θ.
Sine and Cosine
This relationship is expressed by the two most
fundamental equations of trigonometry:
Sin (sine)
is the ratio of the vertical side (the side opposite
the corner we're looking at) to the hypotenuse. Cos (cosine)
is likewise the ratio of the horizontal side (the side adjacent
to that corner) to the hypotenuse. Sine and cosine are functions,
which is to say that they take one number (an angle
in this case, usually expressed in degrees
or radians)
and spit out another. For certain values of θ, it is easy to
figure out what the sine and cosine values are going to be just by
thinking about what the angle corresponds to on the circle; the
simplest cases are for θ = 0°, which is a line
pointing right, giving cos θ = 1 and sine θ = 0; a
line pointing straight up (ie. θ = 90°), which gives
us cos θ = 0 and sine θ = 1, and so on. At
45° the opposite and adjacent sides are the same length, so
from Pythagoras'
Theorem (r2=x2
+ y2) they must each be
(√2)/2. For values in between the sine and cosine vary in a
smooth curve, so that a plot of sin x against x
is your basic wavy line: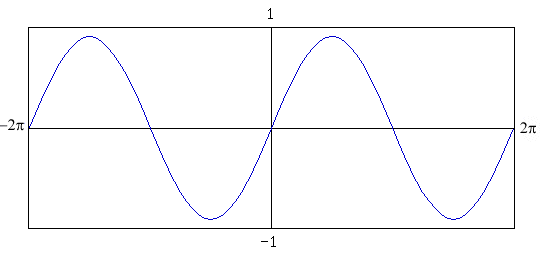
Cosine is to sine as horizontal
is to vertical,
so the graph of cosine is just like the graph of sine shifted by one
quarter-turn. On a graph together, they look like this: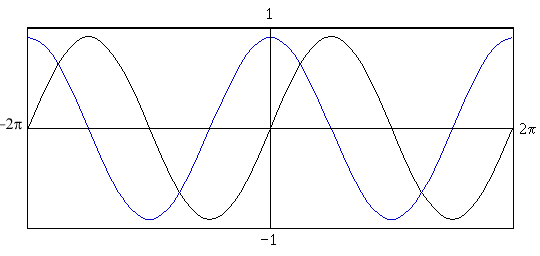
Tangent
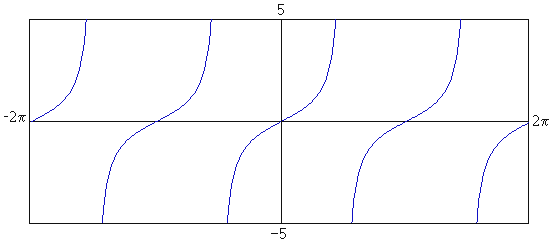
The third basic trigonometric function is called the tangent
(tan
for short), and it is defined as the ratio of the opposite and adjacent
sides - that is:
tan θ = y/x =
sin θ/cos θ
Its graph looks like this:
SOH! CAH! TOA!
So, to recap - the three main trig functions
express the ratios of the sides of triangles like this:
sin θ = opposite hypotenuse
cos θ = adjacent hypotenuse
tan θ = opposite adjacent
Inverse Functions and Reciprocals
If you want to get an angle from two lengths - or,
equivalently, the length of an arc drawn, you need the inverse
functions of sine, cosine and tangent, which are known as arc sine,
arc
cosine and arc
tangent respectively. You may see these written in the form
asin, arcsin or sin-1. Computers can calculate
an angle from two numbers without having to faff around, but as a
legacy from the days before computers the functions conventionally take
a single number, which is the ratio of the two sides relating to the
function you need to use, as in the list above.
For example, in a computer you could input the lengths
of the opposite side and the hypotenuse into the arc sine function to
determine an angle. Using a calculator, you would need to divide the
opposite length by the hypotenuse, and then apply arcsin to the result.
This will give you the angle relative to the quadrant
that you're in, so that you may have to add one, two or three quarters
of a turn to this number, depending on which of the lengths are
negative, if any.
There are three more trigonometric ratios to consider
- the reciprocals of the three basic ones, which is to say the ratios
swapped round. The reciprocal
of something is simply one divided by that thing, so for instance the
reciprocal of 2 is 1/2, the reciprocal of 4/3 is 3/4, and the
reciprocal of 3/4 is 4/3. The trigonometric reciprocals are mainly
useful for simplifying integration
and trigonometric
identities. They are known as cosecant,
secant
and cotangent,
and are defined like this:
cosecant θ = 1 = hypotenuse sin θ opposite sec θ = 1 = hypotenuse cos θ adjacent cotan θ = 1 = cos θ = adjacent tan θ sin θ opposite
More Triangles
So far, I have only talked about trigonometry
as it concerns right-angled triangles and circles. But trigonometry
takes in the study of all kinds of triangles - be they equilateral,
isosceles
or scalene.
Equilateral triangles just have three sides the same length, and three
60° corners. Isosceles
triangles have two sides the same length and hence two identical
angles, so it's easy to split them down the middle and treat them as
two identical right-angled triangles back to back. Scalene
triangles, on the other hand, have every side and angle different, so
if you ever have to calculate their lengths and angles you're likely to
want to use the the
Sine Rule and the
Cosine Rule (unless they happen to be right-angled
scalene triangles, which obviously makes things easier). With three
different angles to work with, it's easiest to call them A,
B and C, and call the
lengths of the sides opposite them a, bc.
The Sine Rule can then be written
a = b = c sin A sin B sin C
This is useful, for instance, if you know two angles
and the length of one side of a triangle, and you need to find the
length of another side; or if you know the lengths of two sides and one
angle (which is not the angle between those sides), and you need to
find one or more other angles. In cases where you have two sides and
the angle between them, or you are given all three lengths and asked to
calculate angles, you will need to switch to the Cosine Rule, which can
be written in two main ways:
a2
= b2 + c2
- 2 × b ×c × cos A
or
b2
+ c2 - a2
cos A = ---------------
2×b×c
The general formula for finding the area of a
triangle is
area = ½ ×
base × height
Which is also equal to
area = ½
× a × b
× sin C.
The choice of which angle in all of these equations is
of course completely abritrary, so feel free to swap around a,
b and c at will, as long
as you also swap A, B and C
to make them fit.
Slopes and Oscillations
Look again at the graphs for sine and cosine; notice
that when one is at an extreme of position, the other is at an extreme
of slope; this observation is important for several reasons. The slope
of the sine curve at any point (which is to say the rate of change of x
with respect to θ) is in face equal to the height of cosine
at that point, if the angle is measured in radians
- this is one of the reasons mathematicians like radians. Similarly,
the slope of the cosine curve at any point is negatively proportional
to the sine.
This means, if you stop to think about it, that the
rate of change of the rate of change at any point (the second differential
of a sine or cosine curve, to use the mathematical term) is always in
negative proportion to its height at that point; it is as if it was
being pushed towards the origin by a force proportional to its distance
from it. In fact, in real life when something is pushed towards a
central point in proportion to its distance from that point (as in pendulums,
weights on springs,
molecules
trapped in solids,
and musical
instruments) it will indeed move in a sine curve, which is
why trigonometry is the mathematics of oscillations
as well as triangles and circles.
The force on a body in simple
harmonic motion is equal to -k × s
where k is a constant depending on the system in
question (the spring
constant in the case of spring
systems) and x is the distance from the
equilibrium point; the position of the body at any moment in time is
given by
x = A
× cos (ω × t )
Where t is time,
ω is the angular
frequency of the motion, which is equal to k2,
and A is the amplitude of the motion.
Waves
A wave is an oscillation which moves in space, such
as sound
waves, earthquake
waves and the matter
waves and light
waves which turn out to make up just about everything in the
universe. Sine waves turn up all over the place; more complex waveforms
can always be broken down into a series of superimposed sine waves of
various frequencies, in a process known as a Fourier
transform. Sub-atomic 'particles' are best thought of as wave
packets.
This extremely general applicability of the idea of
sine waves results in trigonometric functions turning up everywhere you
look in physics. The most general form of the basic wave
equation, appearing everywhere from classical
mechanics through electromagnetism
to quantum
physics, is this:
x = A
× cos (ω × t + d
/ λ)
Where λ is the wavelength
(the distance between one peak of the wave and the next) and d
is the distance along the wave. A full exposition of the mathematics of
waves
is beyond the scope of this writeup; I will just mention quickly that a
fuller understanding of it requires a grasp of the idea of superposition
and interference
- what happens when waves meet each other; refraction
- what happens when a wave passes from one medium
to another; and diffraction
- what happens when a wave passes through a hole. Standing
waves and resonance
are also profoundly important almost everywhere that waves turn up;
they account for the sounds made by different objects, the energies of photon
emitted by different atoms and molecules, and for a staggeringly wide
range of other phenomena.
Infinite Expansions
Interestingly enough, the sine and cosine values of an
angle can be found from the
followinginfinite
series, should you ever need to calculate them from scratch:
The first interesting thing to notice about these
series is that sin θ gets closer and closer to θ as
θ gets smaller. This means that θ turns out to be a
very useful approximation for sin θ at small angles - in
fact, the force pulling a pendulum towards its equilibrium point is
proportional to the sine of its distance from the centre, not directly
to the distance, but it makes remarkably little difference as long as
you don't swing the pendulum too far.
Another interesting thing about the infinite series
for the trig functions is how similar they are to the infinite
expansions of the powers of e,
which is an irrational
number equal to around 2.718. You see, the infinite series
for eθ looks like
this:
eθ = 1 + θ + θ2 + θ3 + θ4... 2! 3! 4!
It is immediately obvious that the form of the
equation is similar. To show us best just how similar it really is, we
need to bring in imaginary
numbers. What we can do is multiply θ
by i
in the expansion (i
is - loosely speaking - the square
root of minus
one; so i
× i
= -1). This gives us the expansion for eiθ:
eiθ = 1 + iθ - θ2 - iθ3 + θ4 + iθ5... 2! 3! 4! 5!
...Which, if you look at it, happens to be equal to
cos θ + i ×
sin θ. This shows clearly the surprising,
but unmistakably logical connection between the complex
numbers and trigonometry, including such gems as Euler's
Identity, the equation linking what may be the five most
important numbers in mathematics:
eiπ + 1 = 0
This connection between the expansions of ex
and the trigonometric functions also brings out the relationship
between trig functions and their kin the hyperbolic
functions, hyperbolic
cosine (cosh)
and hyperbolic sine (sinh),
which - despite their names - otherwise appear quite different.
So...
I hope I have explained, at least in outline, all the
most important things about trigonometry, and made it clear why I think
anyone should care. If any of this seems unclear, I hope the links will
help to fill in any gaps; otherwise, I can be reached by email. There is
much more that I could be saying about the applications of these
functions - besides its basic role in geometry and ubiquitous use in
physics, they turn up all over the place in computer
graphics, in lighting, curves and in strange effects like the Curlicue fractal.
I think that one the best ways to understand
trigonometry are to play around with sine and cosine or to work with
them. If you can program
at all, I encourage you to try making simple pictures or animations by
chucking together trig functions to see what they do; or else, start
with someone else's code (mine,
for instance) and mess around from there. The range of possible effects
is limitless, with beautiful permutations at almost every
turn.
Some
of these permutations are available on t-shirts and other merchandise
at the
Trigonometry shop.
Help
Required from Teachers and Students(in
schools, universities or elsewhere):
I am working on an interactive teaching tool using
Java (or, if you prefer, an educational toy) to help people learn about
waves and especially resonance, in a fun and involving way - please
have a look at Resonata.
It would be very helpful to me to find out more about what sort of
things are already in use in this area, how helpful they are, and who
is being taught what about waves. If you know, I would be very grateful
if you could tell me about it by email.
I'm also very interested in any feedback on this
page - how and why did you find it? Have you found it helpful in
learning, or teaching about trigonometry? If so, was this is in a
formal or informal context? And do you have any suggestions for
improvements?
See also:
My interactive
animations, mostly with source code and almost all largely
based on trigonometric functions
References:
Mannall, G. and Kenwood, M. (1995) 'Heinemann Modular
Mathematics for London AS and A-Level (P2)'. Oxford,
Heinemann Educational Publishers
Stephenson, G. (1995) 'Mathematical Methods for Science
Students'. Harlow, Longman Scientific & Technical
