|
Curlicue |
||
 |
|
|
|
|
The
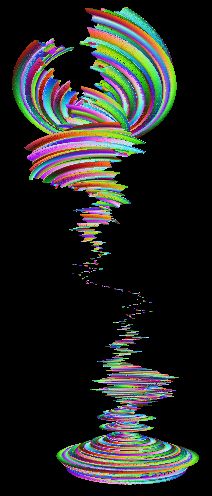
curlicue fractal is an exceedingly easy-to-make but richly complex pattern
composed, at the fundamental level, of Cornu
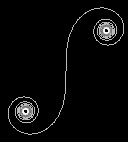
spirals - although that isn't always obvious. The Cornu spiral, also
known as the clothoid or Fresnel spiral, is a sort of S shape that spirals
in on itself at both ends, something like this:
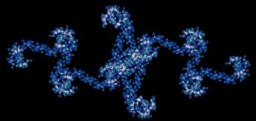
The shape of the fractal varies smoothly as you increase the value of its main input parameter, which makes possible the creation of a perpetually furling-unfurling-spinning animation which cycles through a dizzying array of forms. Every number between 0 and 1 has a different curlicue fractal associated with, the shape of which - for reasons I will get back to - depends on the properties of the number expressed as a fraction. Sometimes it looks like chains of dragons, or seahorses; other times it forms intricate crystalline structures, or shapes which look like nothing more than the spirally doodles of someone with far too much time on their hands. Here is an example of the output from a setting which brings out its true nature particularly clearly - you can see that in some sense it's made out of clothoids in clothoid configurations: I discovered the curlicue fractal when I was very young, playing about in BASIC on a ZX Spectrum - it wasn't until much later that I learnt anything much about what it could do, and why; I don't think I had even heard of fractals when I first stumbled on it, playing around to see what different mathematical functions look like plotted to the screen. I wrote a program that must have looked a lot like this: 10 LET x=128 20 LET y=88 30 FOR f=0 TO 5000 STEP 0.1 40 LET x = x + COS (f*f) 50 LET y = y + SIN (f*f) 60 PLOT x, y 70 NEXT f ...which - to my surprise - drew a series of interconnected spirals on the screen in intriguing configurations. Changing the rate at which f is increased every step turned out to make the whole thing change shape, rather than just changing size as I had thought it might; a small nudge would turn it from a pattern clearly made of interlocking S-shaped spirals to something much harder to characterise, with certain similarities of form but also very striking differences, and more nudges would change it all around again. Since most people these days don't have Spectrums, you might like to play with a version of this in your browser, that runs on Processing.js. At the time I wrote this, what little I knew about the trigonometric functions I was playing with had come from the BASIC manual which came with the computer, and I knew nothing at all of calculus; these equations all seemed quite abstract to me. As a result, a simple description of what was fundamentally being drawn eluded me until somebody else drew my attention to it: This is the trail left by a turtle which takes steps of a fixed size and turns left faster and faster each step. This allows an elegant reformulation of the program which brings out what is really the main input parameter - sticking with Spectrum BASIC for consistency, we can now write* 10 LET x=128 20 LET y=88 25 INPUT seed 26 LET df=0 27 LET f=0 30 FOR i=0 TO 5000 STEP 0.1 35 LET df=df+seed*2*PI 36 LET f=f+df 40 LET x=x+COS f 50 LET y=y+SIN f 60 PLOT x, y 70 NEXT i If the rate of increase of the speed of rotation (the seed for the fractal) is small enough, then the shape traced is essentially a clothoid. However, where a clothoid spirals ever-closer to its focus without ever reaching it, our algorithm sooner or later reaches a point where the fixed size of its steps becomes important, and its path diverges from that of the true clothoid because it cannot follow the tight curve. As the turtle turns ever-faster, it will eventially reach a point where it is turning 90° each step, tracing out a square; then, a little later, it will be jumping over the same three points of an equilateral triangle, then hopping back and forth between two points as it turns right around with each step. After that, the turtle goes through the same sequence on the other side - triangle path, square, pentagon and so on, until it is once again tracing something close to the smooth curve of a clothoid. This is not usually the same clothoid as it came in on - the moment of reversal, where the new clothoid effectively starts, can leave the angle of the new clothoid out of synch with the old one by an amount which depends on where on the new clothoid the turtle starts out. This is where things start to get interesting, because in effect what is happening (for most seeds) is that each of these clothoids takes us one step along a larger one; we soon see a pattern of clothoids made of clothoids. Keep going, and we see that the larger clothoids themselves form even larger clothoids; if the input parameter is an irrational number, we can keep on going, finding ever-larger levels of organisation as we look at the pattern on a larger and larger scale. Why should it matter that the input parameter is an irrational number? Well, remember that the seed value is the amount by which the change in the angle increases every step, as a fraction of a full turn. If the seed is a rational number - that is, if it can be expressed as a fraction - then both the angle and its rate of change are guaranteed to hit a multiple of 2 times pi again after a number of steps equal to the denominator of that fraction if it is odd, or twice the denominator if it's even (the proof of this is left as an exercise for the reader). To take the most basic example, a seed value of a half will have it looping back after four steps - it will take one step, make a half-turn, step, make a full turn, step, and make a full turn and a half, which in terms of what it draws is exactly the same as just taking another half-turn. For some values, it will return to the starting position as well as its original orientation; for most, it will repeat the same few steps ad infinitum as it dances off into the distance. If you can put your finger on what makes the difference between these two sorts of behaviour, you are almost certainly a better mathematician than me. Clearly the form of the fractal reflects the nature of the seed number in various interesting ways, which as far as I know have never been explored in very great depth. It is probably only for irrational seed numbers that it counts as a true fractal - for other input values, any self-similarity will occur on a finite number of levels. Cliff Pickover devotes a chapter of his book Keys to Infinity to the curlicue fractal, exploring the temperature of the curves produced by different seeds, where temperature roughly corresponds to wiggliness**. By this measure the 'coolest' fractal that Pickover could find was the one corresponding to the golden ratio, yet another argument for the specialness of that number - albeit a particularly abstruse one. Animated versions of the curlicue fractal periodically pass through convergence points, where what was a pattern repeating itself through space gradually folds in on itself until all the copies lie on top of each other; then the moment passes, and the copies diverge again - dancing around and outwards in their consistent, yet curiously unpredictable way. I have spent many hours since I first came across the curlicue fractal - too many, probably - playing with it, mesmerised... * We are actually
switching to triangle numbers here - the sum of the series 1+2+3+...n
- instead of squares, which would be the sum of the series 1+3+5+...(2n-1);
the mathematics are similar, and exactly the same kind of fractal is
produced, but the relation of the input seed to the output is somewhat
different.
|
see also:
Downloads: Drag in the main view of the program to rotate the form. Enter a value into the Seed box to see the curlicue associated with that number. Simple fractions correspond to simple forms. Experiment with the other controls to get a feeling for what they do. Note that Piece Size only has an effect with the sphere and cube views. The Trails option may not work as intended on certain systems. Dragoric Dragomatic |